| ONSITE |
- Bring a laptop PC to the class for these experiments. A web browser should be installed.
| ONLINE |
- Use your PC (not smartphone) to join the experiments.
- Note
- This text can be read online:
http://akihikoy.net/p/TULE2
- In these experiments, we explore AI (artificial intelligence) technologies for robot control. Especially we use machine learning and optimization. The task is a throwing motion of a single-finger robot where we control the ball behavior thrown by the robot. When the ball behavior is difficult to analyze, using AI tools is an approach to achieve the task. The goal of these experiments is learning the use of AI technologies under the context of robot control.
Preparation †
| ONSITE | ONLINE |
Install a web browser to your PC. Google Chrome is recommended.
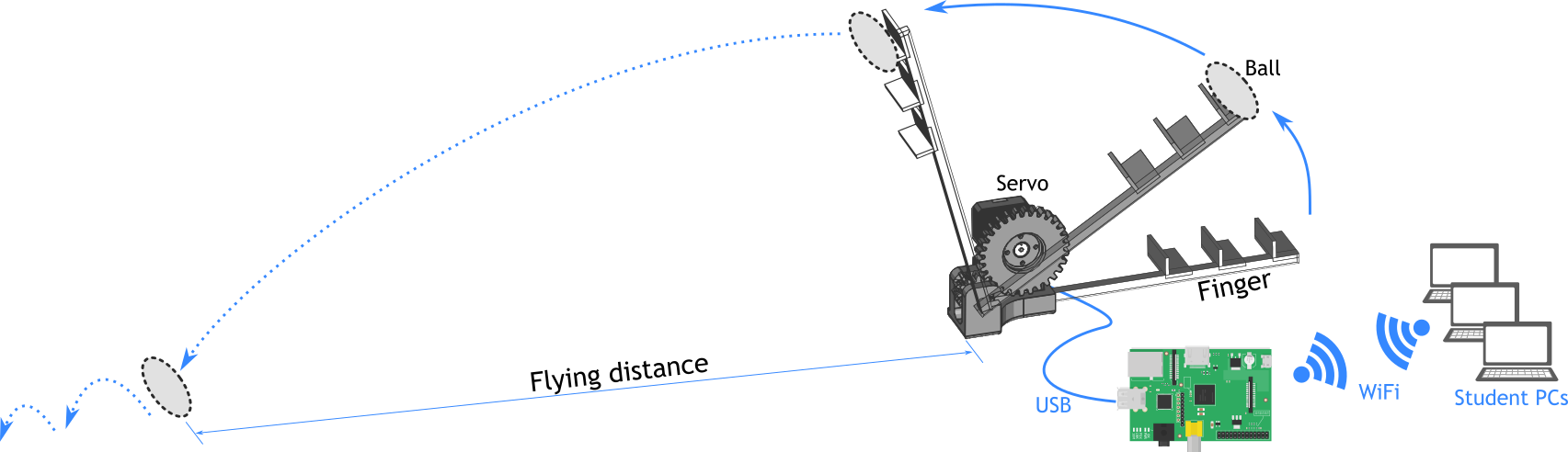
Robot System Overview †
| ONSITE |
The robot we use is a single-finger robot with 1 degree-of-freedom. It consists of 3D printed frames and an actuator, Dynamixel servo motor. The Dynamixel servo is connected to a mini PC (Raspberry Pi 3B) with USB, which is connected to a local network. All programs are installed on the mini PC including the Dynamixel controller and AI tools.
Students connect their PCs to the network over WiFi, and log on to the mini PC from a web browser.
The following figure illustrates the system and the ball throwing task.
| ONLINE |
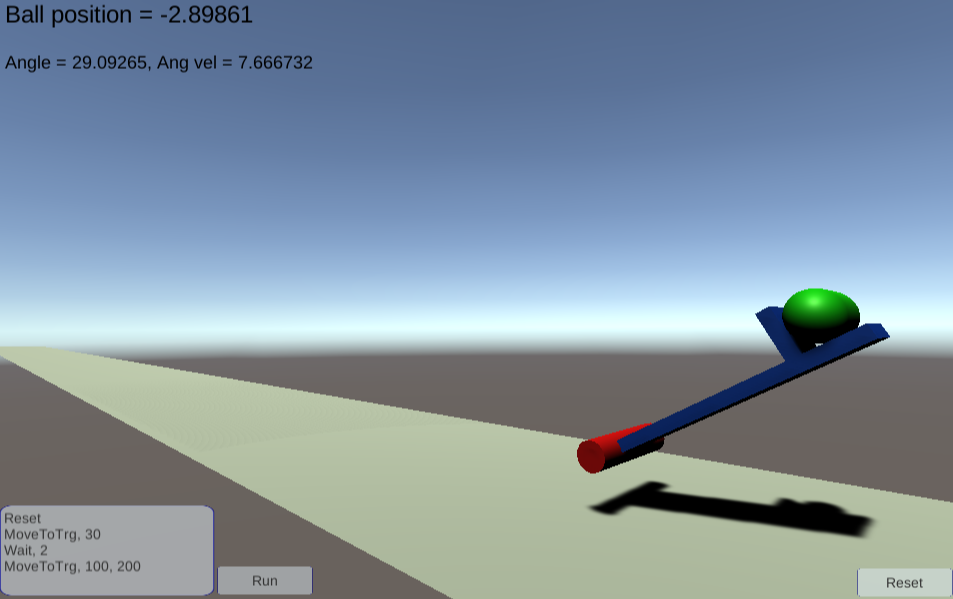
We use a simulation robot similar to the single-finger robot used in the ONSITE experiments. It is implemented with a game engine Unity, and simulating the dynamics of the robot and a ball. You can access to the robot from here:
http://akihikoy.net/p/FingerRobotWebGL/index.html
You can see a text box in the left bottom corner, and the Run button. The text box describes a list of commands to operate the robot. Click the Run button to execute the commands. In default, it moves to the 30 degree position, waits for 2 seconds, and moves to 100 degree with 200 power. You will see that the robot throws the ball, and after a few seconds, the ball lands on the ground. The ball position is always displayed at the left top corner. Once if the ball lands, "First landing position" is displayed, which denotes the flying distance of the ball.
Programming the Robot †
We make programs with Python (a script language) on the mini PC. The Jupyter environment is installed on the mini PC (or your PC, or Colab), which enables us to write and run programs through a web browser.
First Step: Move the Robot to Throw a Ball †
Proceed the following steps with the lecturer:
Hello World †
| ONSITE |
- Connect your PC to the wireless network: ayexp
- Open a web browser on your PC and access:
- http://192.168.11.5X:8888/
- Replace X by the number of the mini PC (find aypiX on the mini PC).
- Type the pass phrase.
- If a message "Please use a different workspace" is displayed, enter a name like "lab2".
- In the directory panel (left side), go to HOME -> prg -> ai_ctrl_1 -> student.
- From the File menu, choose New Launcher.
- Select Notebook -> Python 2 on the right panel.
- Set file name BXXXX_NAME_NAME
- Right click the tab of the file, and select "Rename Notebook".
- BXXXX denotes your student ID.
- NAME_NAME denotes your name in alphabet (e.g. Taro_Yamada).
- Type as follows:
#/usr/bin/python import sys sys.path.append('../sample') from libaictrl1 import * - Press Shift+Enter to run the code block (called cell).
- The above code is for loading the library. It will display nothing, if there is no error.
- You can run the cell again by selecting the cell and pressing Shift+Enter.
- In the next cell, type following:
print('Hello world, my name is XXX XXX, ID: YYY')- Replace XXX XXX by your name (e.g. Taro Yamada) and YYY by your student ID.
- Press Shift+Enter to run the cell.
- You will see the text displayed after the cell.
| ONLINE |
- Open a web browser and access Google colaboratory (Colab, in short): https://colab.research.google.com/
- Clock New notebook, or open an existing file if you want to resume.
- Change the file name to BXXXX_NAME_NAME
- Select File menu -> Rename.
- BXXXX denotes your student ID.
- NAME_NAME denotes your name in alphabet (e.g. Taro_Yamada).
- Type as follows:
!git clone https://github.com/akihikoy/ai_ctrl_1.git - Press Shift+Enter to run the code block (called cell). If the output is like the following, the library is correctly downloaded from GitHub.
Cloning into 'ai_ctrl_1'... remote: Enumerating objects: 129, done. remote: Total 129 (delta 0), reused 0 (delta 0), pack-reused 129 Receiving objects: 100% (129/129), 3.88 MiB | 19.21 MiB/s, done. Resolving deltas: 100% (64/64), done.
- Type as follows:
import sys sys.path.append('ai_ctrl_1/sample') from libaictrl2 import * - Press Shift+Enter to run the code block.
- The above code is for loading the library. It will display nothing, if there is no error.
- You can run the cell again by selecting the cell and pressing Shift+Enter.
- In the next cell, type following:
print('Hello world, my name is XXX XXX, ID: YYY')- Replace XXX XXX by your name (e.g. Taro Yamada) and YYY by your student ID.
- Press Shift+Enter to run the cell.
- You will see the text displayed after the cell.
| ONSITE | ONLINE |
As you have experienced, this environment is a cell-by-cell interpreter programming interface of Python. It is called Jupyter Notebook.
- Exercise
- Play with Python and Jupyter Notebook.
Compute some equations, e.g.
print(np.cos(np.pi)**2)
Tips: Using Jupyter Notebook †
The current cell is highlighted by the left mark. Right click it to see the editing menu. You can also click and drag the cell to change the order of the cells.
- Press Esc,A to add a line above the current cell.
- Press Esc,B to add a line below the current cell.
Throwing a Ball with the Robot †
| ONSITE |
- In the next cell, write the following code and run it.
dxl= SetupRobot()- This code setups the connection with the robot.
You will see the output like:Opened a port: /dev/ttyUSB0 Changed the baud rate to: 57600 Torque disabled Torque enabled
- This code setups the connection with the robot.
- Move the robot to the initial pose by following code:
- Be careful: the robot moves. Hold the base of the robot.
- Note that the robot is shared with the other students. Do it one by one.
MoveToTrg(dxl, 0.2, 1.0)
- Let's throw the ball:
- Place a ball on the robot arm.
- Type the following code and run:
MoveToTrg(dxl, 0.8, 0.7)
MoveToTrg is a function to move the robot to a target position.
MoveToTrg(dxl, d_angle, effort)
where dxl is the variable returned by SetupRobot(), d_angle is the target angle in radian, and effort is torque to use (should be in [0,1]). If effort=0, the robot will not move.
| ONLINE |
Unlike the ONSITE experiments, we cannot operate the robot from the Python program. Instead, we use the command box on the simulator.
Type following commands in the left bottom text box of the simulator.
Reset
MoveToTrg, 30
Wait, 2
MoveToTrg, 100, 200
The command list is described in the CSV (comma-separated values) format. The first value denotes a command type.
There are only three command types: Reset to reset the simulation (the ball position and the robot position are initialized), Wait to sleep before executing the next commands, and MoveToTrg to move the robot.
MoveToTrg is a command to move the robot to a target position.
MoveToTrg, target_angle, effort
where target_angle is the target angle in degree, and effort is maximum force to operate the robot (should be in [0,800]). If effort=0, the robot will loose the power.
Theoretical Overview †
The motion you made in the previous step is a throwing motion, but the ball is not controlled. We are interested in controlling the flying distance of the ball (let's define the distance as the length between the robot mount and the first landing point). The flying distance is decided by several factors:
- Motion of the robot.
- We control the robot with target positions. At least, two target positions are necessary: the initial position and the final position. The motion from the initial to the final positions is controlled by the internal controller of the servo, but you can adjust it by changing the effort parameter.
- Ball property (mass distribution, friction, etc.) that affects ball behavior.
- The elasticity of the robot.
- Air resistance.
Sometimes it is not easy to analyze the dynamics of the robot and the ball with considering all these factors.
Using machine learning tools is a solution.
Especially, we take an approach of model-based reinforcement learning. Refer to literature of machine learning, reinforcement learning, and optimization for the details. Here we describe the ideas briefly:
- We use regression to model the unknown dynamics.
- In this case, the dynamics is a mapping from [input: an initial state and control parameter] to [output: the flying distance].
- Regression is a technology to make such a mapping (estimator from input to output) with pairs of (input, output) data.
- We use optimization to find a control parameter to achieve desired control.
- The goal is throwing a ball to a given target distance.
Regression †
When data of pairs of input x and output y is given ( \((( \mathit{data} = \{x_k, y_k \mid k=1,2,...\} \))) ), creating a model F that estimates y for a given x is called regression:
\$$$ y = F(x) \$$$The model F is trained so that the errors between \((( y_k \))) and \((( F(x_k) \))) are minimized.
The design of the model F varies. A simplest model is a linear model. However the capability of linear models is limited; the modeling error becomes large when modeling nonlinear functions.
There are nonlinear approaches of representing F. The examples are Gaussian processes for regression (GPR) and (artificial) neural networks. In these experiments, we use a version of neural networks, multi-layer perceptron (MLP).
MLP can represent nonlinear functions in general. It has some parameters, including:
- The number of hidden layers and units that are designed by the users.
- Weights of the node connections that are learned from data with the back-propagation method.
Note that although MLP can learn a function where x and y are multidimensional vectors, we consider both x and y are single dimensional.
Optimization †
When an objective function E(x) is given, finding x that minimizes E is called optimization. E is a scalar function while x can be multi-dimensional. E is also called evaluation function, cost function, loss function, etc. Note that maximizing E is the same problem; just consider a negative of E (max E = min (-E)).
When the objective function E is simple, we could solve this problem analytically. However when E is complicated, finding analytic solution becomes difficult. In that case, we can take a numerical optimization approach.
A simple example is hill climbing. We start with a random (or certain) initial value \((( x_0 \))), and compute the gradient of E with respect to x around \((( x_0 \))): \((( \frac{dE}{dx}(x_0) \))). Then modifying \((( x_0 \))) to the negative direction of the gradient, the value of the evaluation function at the modified x becomes smaller. Iterating this updates, we will finally find x that minimizes E.
There are other methods like hill climbing that use gradients. For example gradient descent method, and Newton's method. The back-propagation method used to train MLP is also a gradient method.
A drawback of the gradient method is that it is often trapped by local optima. You can imagine that by assuming E has multiple peak points. This issue sometimes happens when E involves learned models such as MLP.
CMA-ES (Covariance Matrix Adaptation Evolution Strategy) is another approach where we do not have to give the gradient of E. It uses multiple search points (population), which makes it more robust to noisy function than gradient methods.
Model-based Reinforcement Learning for Throwing Motion †
Let us assume a control parameter x that changes the flying distance of the ball thrown by the robot. For example x is an effort parameter.
Let y denote the flying distance.
Let f denote the dynamics, i.e. y = f(x). Note that we give up to model f analytically, i.e. we do not know f.
The ball throwing problem: for a given target of flying distance \((( y_\mathit{trg} \))), find a control parameter \((( x_\mathit{opt} \))) that achieves \((( y_\mathit{trg} \))), i.e. \((( y_\mathit{trg} \approx f(x_\mathit{opt}) \))). Note that we need to solve this problem for any \((( y_\mathit{trg} \))).
The solution idea is as follows:
- Learning phase:
- Throwing the ball with random control parameters and observing the flying distances. We obtain \((( \{x,y \mid k=1,2,...,N\} \))).
- Training an MLP f with the data obtained above.
- Testing phase:
- For a given target \((( y_\mathit{trg} \))), finding a control parameter \((( x_\mathit{opt} \))) such that \((( y_\mathit{trg} \approx f(x_\mathit{opt}) \))). This problem is formulated as an optimization problem, and solved by CMA-ES.
- Executing the solution \((( x_\mathit{opt} \))) and measuring the error to evaluate the performance.
The idea of finding the control parameter with optimization is as follows: We define the objective function as a squared error of \((( y_\mathit{trg} \))) and \((( f(x) \))):
\$$$ f_\mathit{error}(x) = (y_\mathit{trg} - f(x))^2 \$$$We use CMA-ES to minimize this objective function with respect to x. The found x is \((( x_\mathit{opt} \))) that satisfies \((( y_\mathit{trg} \approx f(x_\mathit{opt}) \))).
Report †
The report consists of two parts, and you need to submit both.
- Report of experiments (Score: 80):
- Make a report of the experiments using Jupyter Notebook, and save it as a PDF (cf. Making Report with Jupyter Notebook).
- Language: You may use only English to write this report.
- Report of survey (Score: 20):
- Make a report of a survey related to the experiments.
- Language: English or Japanese.
Deadline †
The deadline of both reports is 1 week after the class.
Submission †
Prepare the report files in PDF format.
- The file name should be: TU_LabExpII-BXXXX_NAME_NAME (YYYY)
- BXXXX: your student ID.
- NAME_NAME: your name as written in the student ID card (e.g. 山田太朗).
- YYYY: EXPERIMENTS or SURVEY (for "Report of experiments", "Report of survey" respectively).
Then use this form to submit: LEII Report submission form
Making Report with Jupyter Notebook †
In the Jupyter Notebook, you can write documents in cells. Use this function to make your report.
In default, the mode of the cell is Code. Change it to Markdown by selecting from the right top list. In Google Colab case, click the +Text icon to add a text cell.
In the markdown cells, we write text with markdown style. Some useful styles are:
# Section header ## Subsection header Normal text.
- List item 1 - List item 2
Press Shift+Enter to convert the plain text to the formatted text.
In the following experiments, insert short notes about the purpose, hypothesis, results of the experiments, and analysis, before and/or after each experiment as the markdown cells.
Finally, select File -> Export Notebook As... -> PDF to save the document as a PDF file. On Google Colab, select File -> Print and select Print to PDF. NOTE: In case generating PDF fails, you may download and upload the ipynb file.
If PDF export or download does not work, export (or download) it as an HTML, and convert it to a PDF by printing the HTML file with a web browser.
Experiments †
We practice the theory mentioned above step by step.
Regression with MLP †
We train an MLP with manually generated data to see how to use MLP. Then we plot the learned function f(x) for visualizing the learning performance.
The steps are:
- Generate data (data_x, data_y) manually.
For example:
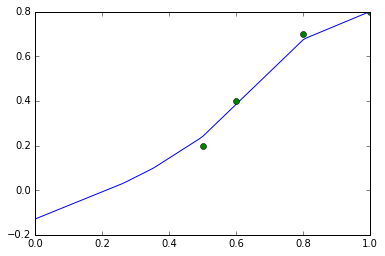
Note: data_x[i] corresponds with data_y[i] (e.g. 0.2 is the output to 0.5).data_x= [0.5, 0.6, 0.8, 1.0] data_y= [0.2, 0.4, 0.7, 0.8] - Train an MLP with (data_x, data_y).
MLPR stands for MLP Regression. This function returns f, which is a function f(x) that returns y.f= TrainMLPR(data_x, data_y) - Test the function f(x) by feeding x that is not in the data.
For example,
(You can omit "print" like this.)f(0.55) - Plot the function f(x).
PlotF plots the function f in the range of [xmin,xmax]. With show=True, it shows the graph immediately, and with show=False, it does not shows the graph until plot.show() is executed. plot.plot adds data points into the graph with the marker 'o'. You will see a graph displayed.plot= PlotF(f, xmin=0.0, xmax=1.0, show=False) plot.plot(data_x, data_y, 'o') plot.show()
- Exercise
- Change the data and other values in the above exercise. Try to learn a nonlinear function.
Optimization with CMA-ES †
We define an objective function f_error as a squared error of a target value y_trg and f(x) learned in the previous step. Then we minimize f_error with respect to x with CMA-ES.
The steps are:
- Define the objective function f_error.
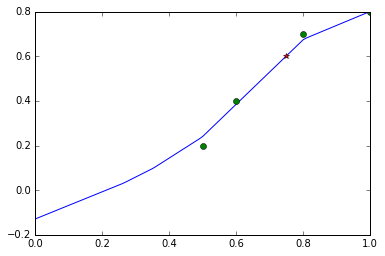
This is the function definition of Python style. Note that in Python, the indent is important.def f_error(x): y_trg= 0.6 return (y_trg-f(x))**2 - Minimize f_error to find x_opt.
The FMin function uses CMA-ES to minimize the given function. 0.5 is the initial value, and [0.0, 1.0] is the search range (see below).x_opt= FMin(f_error, 0.5, 0.0, 1.0) - Print values of x_opt, f(x_opt), and f_error(x_opt) to see if the optimization succeeded.
print('Solution:', x_opt, f(x_opt), f_error(x_opt)) - Plot a graph of f(x) with the optimized value (x_opt, f(x_opt)).
We are plotting f(x), the training data with markers 'o', and the optimized value with marker '*'.plot= PlotF(f, xmin=0.0, xmax=1.0, show=False) plot.plot(data_x, data_y, 'o') plot.plot([x_opt], [f(x_opt)], '*') plot.show()
- Exercise
- Change the target value y_trg. Use the MLP trained in the previous experiment.
Reference: FMin †
FMin(f, x_init, x_min, x_max)
where f is the function to be minimized, x_init is the initial value of search, [x_min,x_max] is the search range.
Learning Dynamics of Throwing Robot †
Let's do the above things with data obtained from the real robot.
The steps are:
- Repeat N times:
- Throw the ball with random control parameter x.
- You can decide the control parameter as you like. A way is defining it as the effort parameter.
- Observe the flying distance as y.
- Put x, y in the list data_x, data_y respectively (just write them manually in the code).
- NOTE: Too large / small values of x and y will affect learning and optimization since sometimes these algorithms assume a range of the values. In such a case, consider to scale the data. A simple way of scaling is:
data_x= [100, 200, 400, 600] data_y= [20, 30, 40, 50] data_x= np.array(data_x)*0.001 data_y= np.array(data_y)*0.1
- NOTE: Too large / small values of x and y will affect learning and optimization since sometimes these algorithms assume a range of the values. In such a case, consider to scale the data. A simple way of scaling is:
- Throw the ball with random control parameter x.
- Train MLP with data_x, data_y and obtain f(x).
- Plot the function f(x).
- Exercise
- Complete the above steps.
| ONSITE |
- Hint
-
For collecting data, create two cells:
MoveToTrg(dxl, 0.2, 1.0)
Run the first cell to move the robot to the initial position. Place the ball. Edit x (control parameter; here, we define it as the effort parameter). Press Shift+Enter to run the second cell. Measure the landing point of the ball (flying distance) as y. Add the values of x and y to the list by manual. Repeat these steps for N times.x= 0.9 MoveToTrg(dxl, 0.8, x)
| ONLINE |
Control the Robot to Throw the Ball to a Target Location †
Refer to the experiment of Optimization with CMA-ES, make a program to throw a ball to a target location.
The steps are:
- Define the objective function f_error with y_trg.
- Minimize f_error to find x_opt.
- Print values of x_opt, f(x_opt), and f_error(x_opt) to see if the optimization succeeded.
- Plot a graph of f(x) with the optimized value (x_opt, f(x_opt)).
- Execute the solution x_opt.
- Measure the flying distance and compare it with y_trg.
- Exercise
- Complete the above steps. Repeat the above several times with different y_trg. Evaluate the control accuracy.
- Hint
- You can calculate the mean and the standard deviation with NumPy (imported as np) like this:
result_y=[0.5, 0.6, 0.45, 0.8] print('Average:', np.mean(result_y)) print('Standard deviation:', np.std(result_y))
Survey [UPDATED] †
- Choose one or two topics to survey:
- Reinforcement learning for robots.
- Model-based and model-free reinforcement learning (advantages, disadvantages).
- Recent research of robot learning and AI.
Programs and CAD Models †
The programs and CAD models of the robot are available on GitHub:
https://github.com/akihikoy/ai_ctrl_1
Notes for TA †
Setup before the Experiments †
| ONSITE |
- Place three Raspberry Pis and three robots.
- Make three pairs of (Raspberry Pi, finger robot) where the robot is connected to Raspberry Pi with USB.
- Connect micro USB power supply to Raspberry Pi to turn on it.
- For each Raspberry Pi (X=6,7,8):
- Log in to Raspberry Pi over SSH.
- IP: 192.168.11.5X where X is the number of raspi (aypiX).
- User: hm
- Turn on JupyterLab:
- .local/bin/jupyter lab
- Log in to Raspberry Pi over SSH.
Shutdown †
| ONSITE |
- For each Raspberry Pi (X=6,7,8):
- Close JupyterLab by pressing Ctrl+C.
- Shutdown Pi.
- sudo shutdown -h now
Using Anaconda †
Prepare a PC (Windows/MacOS/Linux), and follow the instruction:
- Install Anaconda. Anaconda is a free and open-source distribution of the Python language for data science. By installing this, you can install Python, the Jupyter environment, and some Python libraries needed for the experiments (numpy, scipy, scikit-learn, Matplotlib).
- Visit https://www.anaconda.com/
- Open the page: Products -> Individual Edition
- Download an installer for your OS. 64-bit Windows user: Windows / Python 3.8 / 64-Bit Graphical Installer (466 MB)
- Run the installer.
- Download the ai_ctrl_1 library. ai_ctrl_1 is a library for this course.
- Download the GitHub repository as a zip file https://github.com/akihikoy/ai_ctrl_1
You can use this direct download link: https://github.com/akihikoy/ai_ctrl_1/archive/master.zip - In your home folder, make a folder named Jupyer.
- Extract the ai_ctrl_1-master folder in the zip file into the Jupyer folder.
- Download the GitHub repository as a zip file https://github.com/akihikoy/ai_ctrl_1
- Test Jupyter Notebook. Jupyter Notebook is an interactive programming environment over a web browser.
- Run Jupyter Notebook (Windows user may find it in the start menu).
- Access http://localhost:8888/
- If you can see files in your home folder, Jupyter Notebook is working.
- Browse folders: Jupyter -> ai_ctrl_1-master -> student
- Click the New button around right top corner, and choose Python3.
- You should see a prompt like: In [ ]: [_____]. Then type as follows, and press Shift+Enter. If no error is shown, the installation is completed.
#/usr/bin/python import sys sys.path.append('../sample') from libaictrl2 import *